Γραμμικές απεικονίσεις
Ορισμός
Έστω V, W δύο διανυσματικοί χώροι ορισμένοι στο ίδιο σώμα K. Μία απεικόνιση
T : V → W λέγεται γραμμική αν για κάθε x, y ∈ V και για κάθε λ ∈ K ισχύουν
i. (Προσθετική) T(x + y) = T(x) + T(y),
ii. (Ομογενής) T(λx) = λT(x).
Παρατηρήσεις:
Οι σχέσεις (i.), (ii.) του παραπάνω ορισμού είναι ισοδύναμες με την
T(λx + μy) = λT(x) + μT(y).
T(0V ) = 0W .
Γραμμικές απεικονίσεις και γραμμικοί συνδυασμοί:
T(λ1×1 + λ2×2 + · · · + λk xk ) = λ1T(x1) + λ2T(x2) + · · · + λkT(xk ).
Παραδείγματα:
i. (Διαστολή/Συστολή) T : V → V με T(v) = kv, για κάθε v ∈ V και κάποιο
συντελεστή k ∈ K.
Πράγματι, T(λx + μy) = k(λx + μy) = λ(kx) + μ(ky) = λT(x) + μT(y),
ώστε T γραμμική.
ii. (Μηδενική απεικόνιση) T : V → W με T(v) = 0, για κάθε v ∈ V.
Πράγματι, T(λx + μy) = 0 = 0 + 0 = λ0 + μ0 = λT(x) + μT(y), ώστε T γραμμική.
Παραδείγματα:
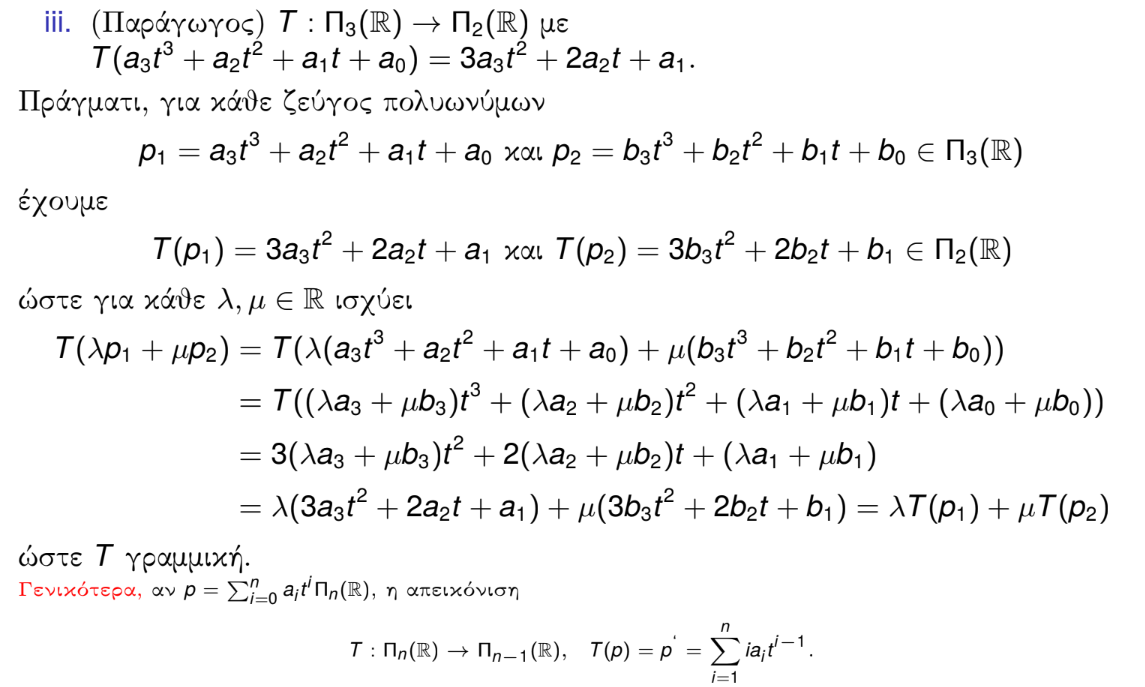

Παραδείγματα:
viii. T : Mn×1 → Mm×1 με T (x) = Ax για κάποιον πίνακα A ∈ Mm×n.
Η γραμμικότητα του μετασχηματισμού έπεται άμεσα από τις ιδιότητες του
πολλαπλασιασμού πινάκων:
T(λx + μy) = A(λx + μy) = λAx + μAy = λT(x) + μT(y).
Θα δούμε ότι κάθε γραμμική απεικόνιση Τ: Κn->Km γράφεται ως πολλαπλασιασμός από αριστερά με κατάλληλο m x n πίνακα.
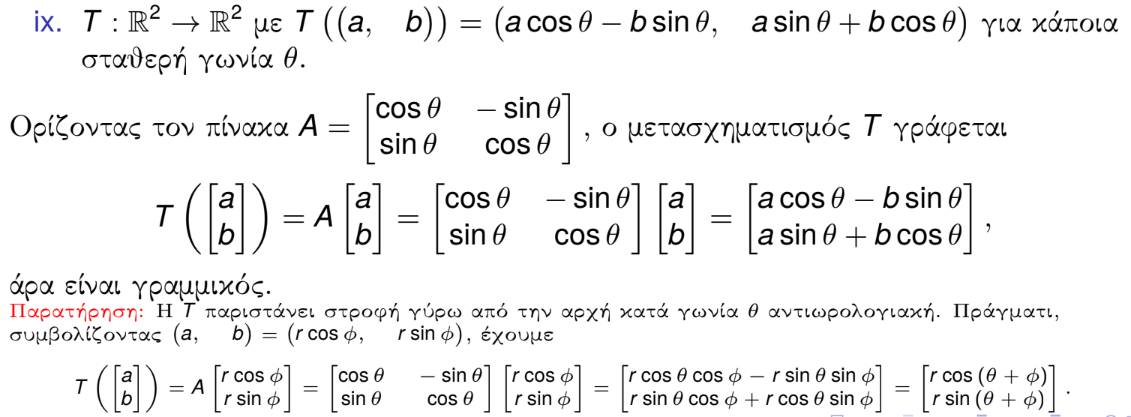
Αντιπαραδείγματα

